PaliGemma
用pytorch从零实现的视觉大模型
本文要讨论的几个主题:
- 视觉transformer
- 对比学习
- 语言模型
- KV-Cache
- 旋转位置编码
- 正则化和评估
先来一张经典图镇楼:
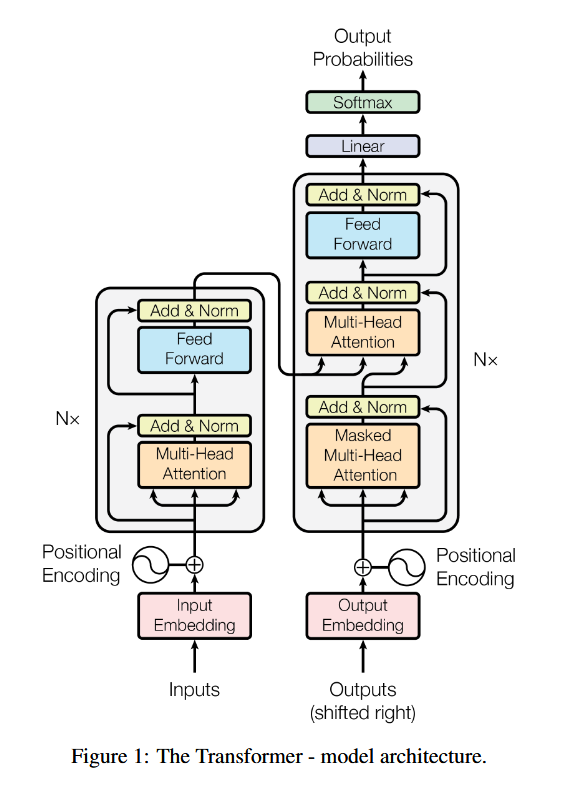
本文总览:
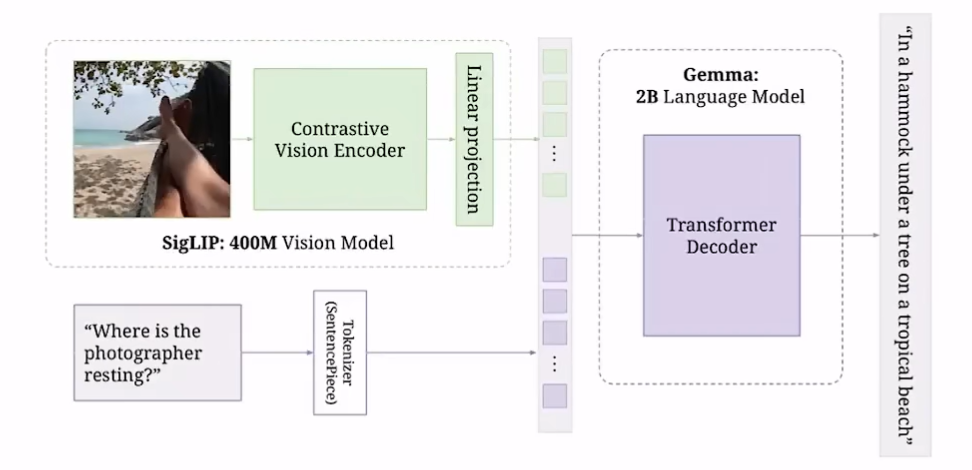
对比学习:
clip视觉大模型采用了这种技术,其实就是如下图:
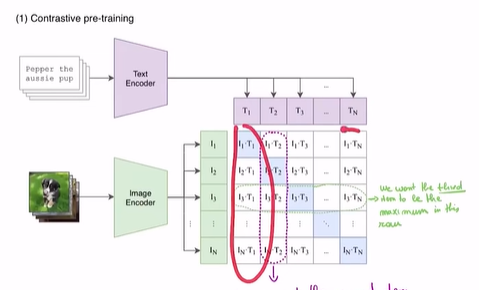
然后希望每一行每一列都接近其他全0,i*i的地方是1。
采用的对比输出和预期分布的损失是cross_entropy_loss,并一般使用 LogSoftmax(为了数值稳定性优化,因为softmax要求指数,结果可能很大,超出32位整数范围)
但是softmax这种处理方法存在一个问题,即计算开销大,而且如果想并行,那么一整行的数据必须保存在一个机器上,这给并行计算也带来了困难。因此也有人建议采用sigmod来处理,sigmod的好处是,将每个格子的值看成一个二分类概率,每个格子值的计算不用依赖其他的格子值,因此简单很多。(这也就是siglip)
为什么非要对比学习,而不是直接让视觉transformer直接学习图片的表示?因为视觉多模态模型里,视觉transformer和语言transformer的编码最后是要拼在一起的,我们希望对图片和文本的编码尽可能对齐,而对比学习起到了对齐的效果,同时这种对比学习无监督,而且训练数据好获得。
对比:两种正则化
Batch Normalization和Layer Normalization
- Batch Normalization (BN):
- 在Batch维度归一化,依赖Batch内其他样本。
- 不适合变长序列或小批量训练(如NLP任务)。
- 同时由于把所有样本的某一维度混合起来了,所以并未完全缓解协变量偏移,需要较大的batch-size
- Layer Normalization (LN):
- 在特征维度归一化,独立处理每个样本。
- 更适合NLP、RNN、Transformer等场景。
语言大模型最后的输出中,每个位置的向量含有前面所有词的信息,而视觉的embeding中每个位置的向量含有所有像素的信息
视觉大模型中encoder layer的结构:
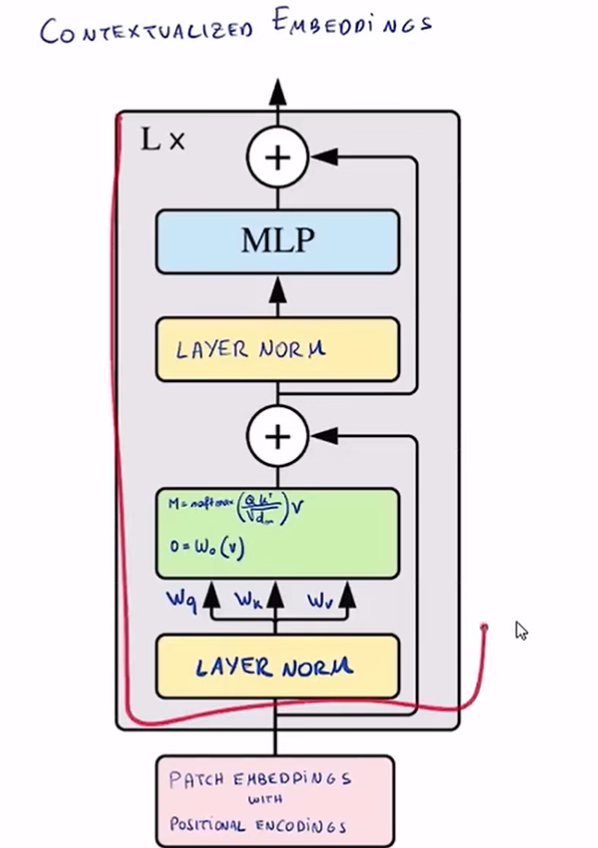
其中,重点还是attention,attention的实现也最复杂,但是本质上也就是张量运算
q,k,v可以理解成注意力机制从三种不同的角度看待一个序列
所谓多头注意力,其实就是把一个embeding的表示(如1024维的向量),分成n个部分,然后每个q,k,v都只关注其中一部分进行注意力计算,最后混合起来
多头注意力的优势:
- 可以并行计算缩放点积注意力
- 多头注意力带来了对某两个词的关联的不同的计算方式(如果只有一个头,那就只能把两个大向量做点积),这可以使得模型学到更好的有关上下文的信息
$$
\text{softmax}(\frac{QK^T}{\sqrt d})V
$$
这个公式的直观理解:softmax后的输出代表了权重,即这个注意力头认为,对V里面的序列(序列里每个值代表一个单词或者一个像素)应该分配多少的权重。
如果是只使用decoder的语言模型,其实内部结构和刚刚上面那个encoder很像了,只是把多头注意力改成了masked multi-head attention。
最后如何将视觉embeding和文本embeding合并到一起?其实就是简单拼起来(paligemma是先创建一个文本的embeding,但是这个embeding前面空了很大的区域用一个<image>的标记来占位,最后把图片填充到这个占位的地方,但是个人感觉直接两个分别计算然后再拼一起似乎也没问题)
KV cache
思想:
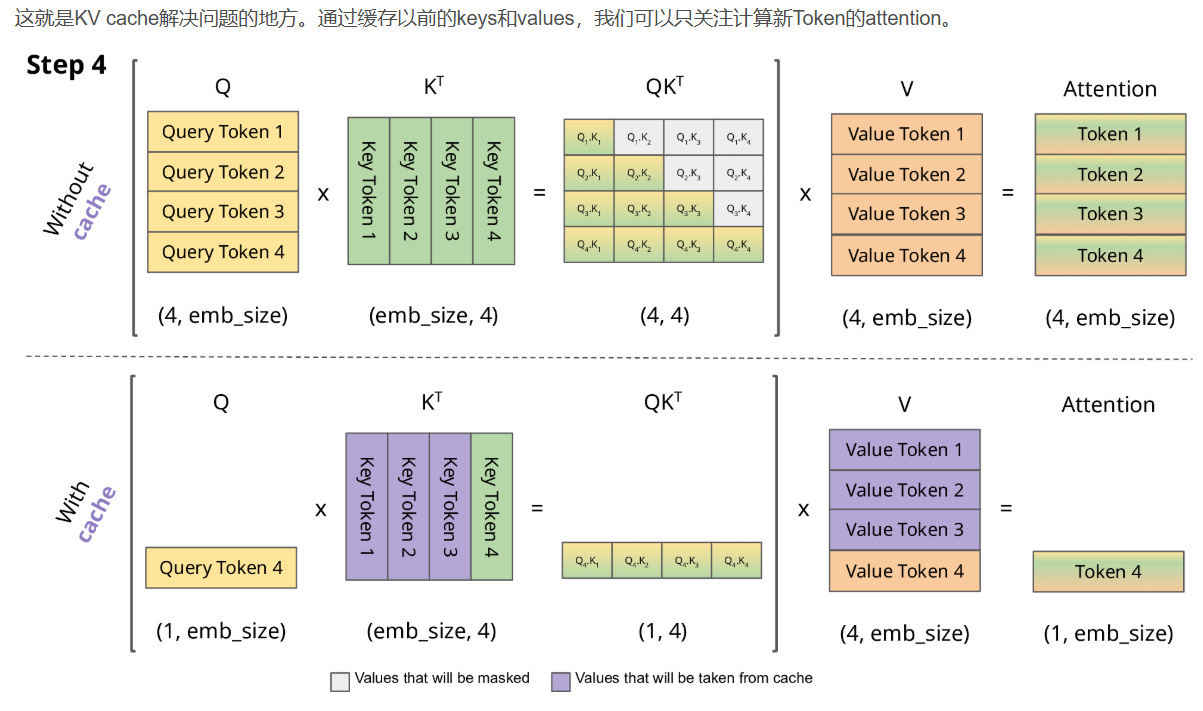
既然每次预测下一个token只使用最后一个token的输出embeding表示,那么为什么还要每次都计算前面的embeding呢?
将KV向量保存下来便于后续计算,这样每次生成后,下次输入模型的也只是最后一个token
分两步:预填充和token生成
过程见下图图示:
RMS norm
在layer_norm之后又提出的新norm方法,思路是:归一化时,保持方差不变很重要,但是保持均值为0似乎没有必要(也已经在实验上验证),因此与其算均值和标准差这两个统计量,不如只算一个统计量:均方根统计量
$$
\text{RMS}(a) = \sqrt (\frac{1}{n}\sum_{i=1}^{n}a_i^2)
$$
分组查询注意力
即当query的数量和key-value的数量不一致时
为了解决计算数据传输的问题:多头注意力计算的瓶颈不在于做了多少点积,而在于将内存从高带宽内存(GPU中的内存)复制到本地内存的时间,那么怎么减少数据传输?
方案:不同的查询头共享键-值头,即键头数量小于查询头,比如2:8
优劣:
- 减少了数据传输量
- 减少的KV-cache的内存量
- 当然不可避免的导致模型表现有所下降(但权衡之后可以接受)
旋转位置编码
RoPE 具有更好的外推性,即在训练时和预测时的输入长度不一致时,更好的避免模型的泛化能力下降。
思想:
- 不直接把位置编码加到token里,而是修改注意力机制,使注意力机制能考虑token的位置信息
- 具体的说,是使得QK^T的点积中能够蕴含相对位置信息。(使点积结果与两个token值,以及相对位置这三个变量决定)
计算公式:不赘述了,这篇文章讲得很好
不过想在这里顺便提一句经典的Sinusoidal 位置编码,为什么使用它:
位置编码的数学定义为:
$$
\text{PE}(pos, 2i) = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)
$$
$$
\text{PE}(pos, 2i+1) = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)
$$
其中:
• pos:序列中的位置(如第 0、1、2 个 Token)。
• i:维度索引(从 0 到 d_model/2-1)。
• d_model:模型的隐藏层维度(如 512、768 等)。
为什么要这样定义:
- 具有远程衰减的性质,即如果是两个相同的词向量,那么他们距离越近,内积分数越高
- 采用正弦余弦,可以表示相对位置关系。如位置
pos + k的编码可通过位置pos的编码线性变换得到 - 一个embeding的不同维度(即pos固定,i变化)可以关注不同的信息:
- i较小时,sin和cos函数的周期小,频率高,捕捉局部依赖
- i较大时,sin和cos函数的周期大,频率低,捕捉长程依赖(即要隔好几个pos才回到同一函数值,内积才会相近)